• Facebook
• Instagram
• Twitter

接續上次【Python】Binary Search Tree (二元搜尋樹) 資料結構實作(1) 接續來講"Delete"的功能，還沒有看過的可以趕緊補上。

其他資料結構通道：
1. 【Python】Stack(堆疊) 資料結構實作
2. 【Python】Single Linked List(單向鏈結串列) 資料結構實作
3. 【Python】Binary Search Tree (二元搜尋樹) 資料結構實作(1)

前言

在 Binary Search Tree 當中，實作刪除節點可以分為以下三個狀況，但在介紹這三個狀況前有些前置作業。

延續上次程式碼【Python】Binary Search Tree (二元搜尋樹) 資料結構實作(1)，我們在 node 新增一個指標 self.parent = None ，讓每個node都可以指向自己的parent，如果沒有parent，代表該node為root node。

class Node:
    def __init__(self, value=None):
        self.value = value
        self.left_child = None #smaller
        self.right_child = None #greater
        self.parent = None # pointer to parent node in tree

在_insert() function 中新增 cur_node.left_child.parent = cur_node 及 cur_node.right_child.parent = cur_node ，讓每字插入node 時每個node都有自己的parent

def _insert(self, value, cur_node):
    if value < cur_node.value:
        if cur_node.left_child == None:
            cur_node.left_child = Node(value)
            cur_node.left_child.parent = cur_node #set parent
        else:
            self._insert(value, cur_node.left_child)


    elif value > cur_node.value:
        if cur_node.right_child == None:
            cur_node.right_child = Node(value)
            cur_node.right_child.parent = cur_node #set parent
        else:
            self._insert(value, cur_node.right_child)


    # value == cur_node.value
    else:
        print("This value has existed

建立好parent的架構之後來談談刪除節點的三個狀況:

狀況一：刪除節點沒有子節點

在刪除節點沒有子節點的情況下， 只要將該節點指向None解決

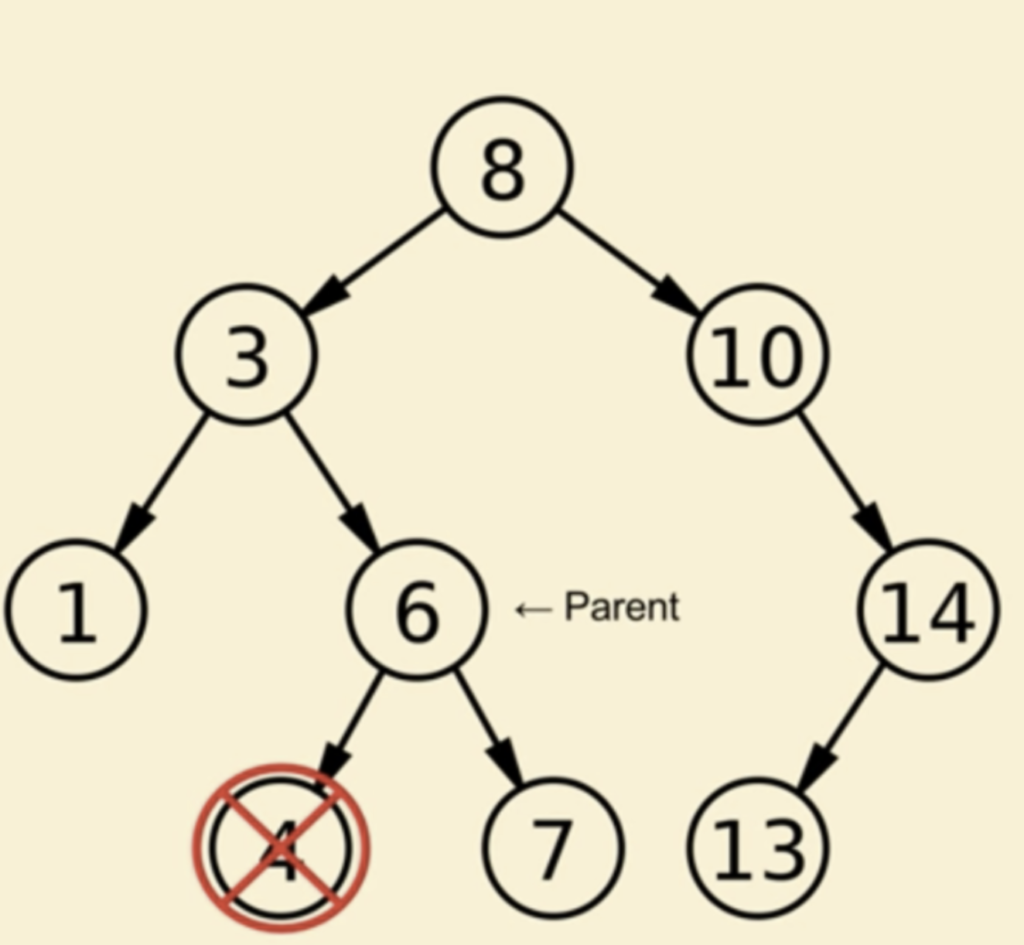
狀況二：刪除節點有「1」子節點

在刪除節點有「1」子節點的情況下，如圖可以發現，將14刪除的話，13的parent會從14變成10，也就是說，刪除14後，10的 right child 會指向13 (記得right node 永遠比 parent大)

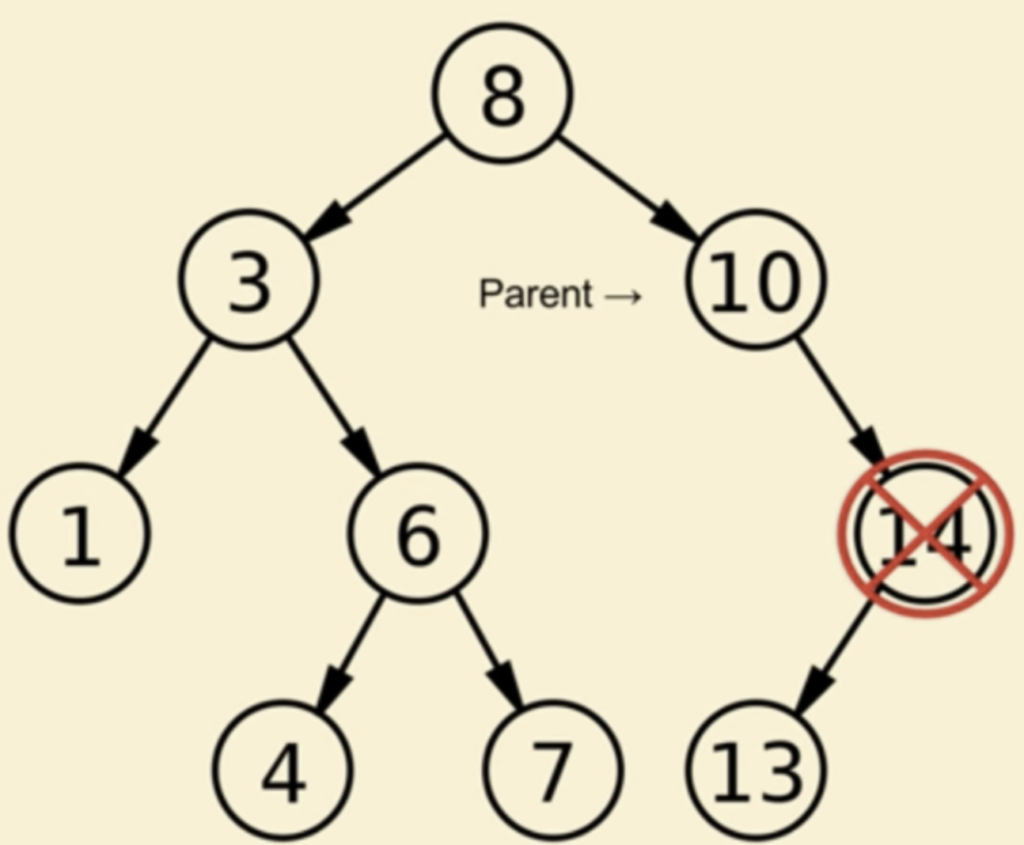
狀況三：刪除節點有「2」子節點

這裡比較複雜，我們要先定一個successor node 也就是要刪除的node的right child，要刪除的node的value等於 successor node 的value，接著就會遞迴呼叫delete function直到successor的 left child指向None。

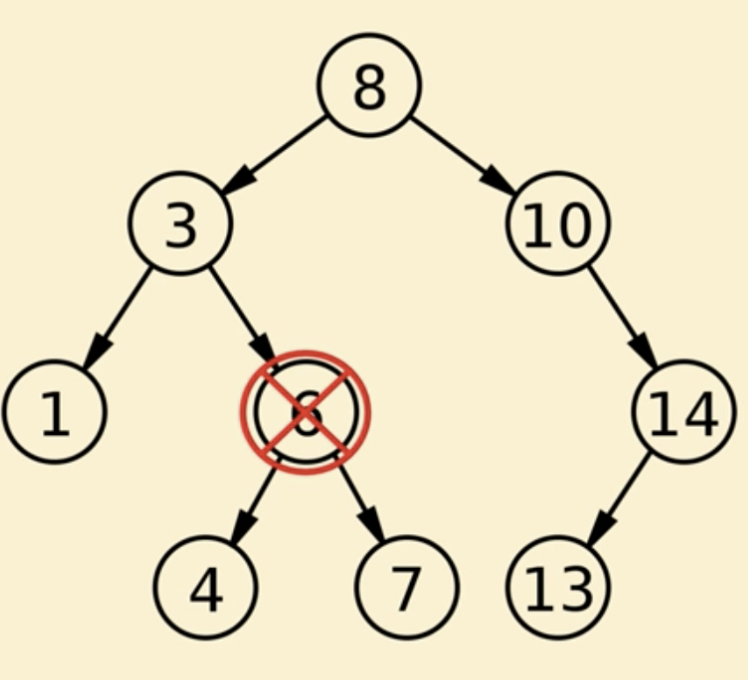
完整程式碼

class Node:
    def __init__(self, value=None):
        self.value = value
        self.left_child = None #smaller
        self.right_child = None #greater
        self.parent = None # pointer to parent node in tree


class Binary_search_tree:
    def __init__(self):
        self.root = None


    def insert(self, value):
        #判斷tree是否為空
        if self.root == None:
            self.root = Node(value)
        else:
            self._insert(value, self.root)


    def _insert(self, value, cur_node):
        if value < cur_node.value:
            if cur_node.left_child == None:
                cur_node.left_child = Node(value)
                cur_node.left_child.parent = cur_node #set parent
            else:
                self._insert(value, cur_node.left_child)


        elif value > cur_node.value:
            if cur_node.right_child == None:
                cur_node.right_child = Node(value)
                cur_node.right_child.parent = cur_node #set parent
            else:
                self._insert(value, cur_node.right_child)


        # value == cur_node.value
        else:
            print("This value has existed")


    def print_tree(self):
        if self.root!=None:
        	self._print_tree(self.root)


    def _print_tree(self,cur_node):
    	if cur_node!=None:
        	self._print_tree(cur_node.left_child)
        	print(str(cur_node.value))
        	self._print_tree(cur_node.right_child)






    def height(self):
        if self.root != None:
            return self._height(self.root,0)
        else:
            return


    # 我們要在每一次遞迴呼叫時傳入cur_height，如果沒有像parameter
    # 樣傳入或儲存成global variable會造成 無法儲存cur_height
    def _height(self, cur_node, cur_height):
        if cur_node == None:
            return cur_height #0
        # 找一個最高的子樹
        left_height = self._height(cur_node.left_child,cur_height+1)
        right_height = self._height(cur_node.right_child,cur_height+1)


        return max(left_height, right_height)


    # returns the node with specified input value
    def find(self, value):
        if self.root != None:
            return self._find(value, self.root)
        else:
            return None


    def _find(self, value, cur_node):
        if value == cur_node.value:
            return cur_node
        elif value < cur_node.value and cur_node.left_child != None:
            return self._find(value, cur_node.left_child)
        elif value > cur_node.value and cur_node.right_child != None:
            return self._find(value, cur_node.right_child)


    def delete_value(self, value):
        return self.delete_node(self.find(value))


    def delete_node(self, node):
        #returns the node with min value in tree rooted at input Node
        #we will pass the single node to treat as the root of a binary search fill_tree
        def min_value_node(n):
            current = n
            # traverse down to the left of the tree until it finds the smallest element returning this value
            while current.left_child != None:
                current = current.left_child
            return current

            #returns the number of children for the specified node
            # return the number of the children and attach the input node either 0,1 or two
        def num_children(n):
            num_children = 0
            if n.left_child != None:
                num_children += 1
            if n.right_child != None:
                num_children += 1
            return num_children


        #create variable to hold both the parent of the node to delete as well as
        #the number of children get the parent of the node to be deleted
        node_parent = node.parent


        #get the number of children of the node to be deleted
        node_children = num_children(node)


        #break operation into different cases based on the
        #structure of the tree & node to be delete


        #CASE 1 (node has no children)
        if node_children == 0:
            #remove reference to the node from the node_parent
            if node_parent.left_child == node:
                node_parent.left_child = None
            else:
                node_parent.right_child = None


        #CASE 2 (node has a single child)
        if node_children == 1:


            # get the single child node
            if node.left_child != None:
                child = node.left_child
            else:
                child = node.right_child


            #replace the node to be deleted with its child
            if node_parent.left_child == node:
                node_parent.left_child = child
            else:
                node_parent.right_child = child


            #correct the parent pointer in node
            child.parent = node_parent


        #CASE 3 (node has two children)
        if node_children == 2:


            # get the inorder successor of the deleted node
            successor = min_value_node(node.right_child)


            #copy the inorder successor's value to the node formerly
            #holding the value we wished th delete
            node.value = successor.min_value_node


            #delete the inorder successor now that it's value was
            #copied into the other node
            self.delete_node(successor)
    def search(self, value):
        if self.root != None:
            return self._search(value, self.root)
        else:
            return False


    def _search(self, value, cur_node):
        if value == cur_node.value:
            return True
        elif value < cur_node.value and cur_node.left_child != None:
            return self._search(value, cur_node.left_child)
        elif value > cur_node.value and cur_node.right_child != None:
            return self._search(value, cur_node.right_child)
        else:
            return False


def fill_tree(tree, num_elems=10, max_int=50):
    from random import randint
    for _ in range(num_elems): #10個 value
        cur_elem = randint(0, max_int) #隨機0~50(不含50)的值
        tree.insert(cur_elem)
    return tree


#============================================================
#建立1~9的樹
tree = Binary_search_tree()
for num in range(10):
    tree.insert(num)


#delete node 5
tree.delete_value(5)

#印出樹
tree.print_tree()

結語

Binary Search Tree 的實作到這邊差不多一個段落

邊筆記邊學習

把一個紀錄視為一個結果

累積起來就有舉足輕重的地位

Practice makes perfect.

你可能會喜歡：
【2020】我的Python學習心路歷程
【Django】用Plotly在django中顯示圖表
【Python】畫三角形、菱形、直角三角形
【Python】Stack(堆疊) 資料結構實作
【Python】Single Linked List(單向鏈結串列) 資料結構實作
【Python】Binary Search Tree (二元搜尋樹) 資料結構實作(1)

推薦入門書籍

精通 Python：運用簡單的套件進行現代運算（第二版）

之前開始入坑python時就是用這本打底的（有換封面過）

這本書除了前幾張介紹基本的語法之外

後續幾張開始介紹與python相關的延伸性的功能

非常適合程式設計初學者以及剛要開始學習這個語言的讀者

羅列以下幾點關於本書大綱供大家參考

• 學習簡單的資料類型、基本數學運算與文字操作 
• 以Python的內建資料結構處理資料 
• 探索Python程式碼結構，包括函式的使用
• 使用模組與套件編寫大型Python程式
• 深入討論物件、類別與其他物件導向功能
• 檢視一般檔案、關聯式資料庫與NoSQL的儲存機制 
• 使用Python建構web用戶端、伺服器、API與服務 
• 管理系統工作，例如程式、程序與執行緒
• 瞭解並行處理與網路程式設計的基礎

---

流暢的 Python：清晰、簡潔、有效的程式設計

適合已經有Python程式語言基礎的人

這本書更詳細的介紹有關python的用法

讓我們寫的程式可以更加"Pythonic"

建議可以與英文版同時閱讀

以後在查閱stackoverflow文獻的時候能不因語言而產生隔閡

• Python 資料模型：瞭解特殊方法是讓物件具備一致行為的關鍵
• 資料結構：充分使用內建的型態，並瞭解 Unicode 時代中，文字 vs. bytes 之間的關係
• 函式就是物件：見識 Python 函式是一級物件，並瞭解這個事實如何影響熱門的設計模式
• 物件導向的習慣用法：學習參考、可變性、介面、運算子多載與多重繼承，並建構類別
• 控制流程：藉由 concurrent.futures 與 asyncio 套件，來充分活用情境管理器、產生器、協同程序與並行
• 中繼編程：瞭解特性、屬性描述器、類別修飾器與中繼類別的工作原理

---

Python 自動化的樂趣：搞定重複瑣碎&單調無聊的工作(第二版)

如果想使用自動化來增強工作流程效率，大推本書

之前這本書只有英文版

在博客來等了1個月還是沒等到

沒想到在2020/08/28 出了中文版

二話不說馬上看看人家都是怎麼用python來完成例行公事的

除了運用Python寫出程式，在幾分鐘內搞定人工手動處理需要花費數小時的工作。

探索Python豐富的模組程式庫來完成某些特定工作

例如從網站上抓取資料、讀取PDF和Word文件，以及自動化執行滑鼠點按和鍵盤輸入的工作。

　‧在一個或多個檔案中搜尋文字
　　‧建立、更新、搬移和重新命名檔案和資料夾
　　‧搜尋網頁和下載網路上的圖文內容
　　‧處理PDF檔的分割與合併，加入浮水印和加上密碼等作業
　　‧傳送Email和簡訊
　　‧填寫線上表單

• 
  【SSH】製作SSH key教學
  製作SSH key 1. 打開終端機(Bash/Terminal) 2. 輸入指令 3. 將指定的 SSH 私 … 閱讀全文
• 
  【快速架站】什麼是Hexo? 5分鐘快速架站教學
  What is Hexo? Hexo 是一個快速、簡單且強大的網誌框架。Hexo 使用 Markdown（或其 … 閱讀全文
• 【Python】Quick Sort 快速排序｜演算法介紹、新手快速入門
  目錄 基本概念實際應用線上學習平台推薦udemy推薦入門書籍精通 Python：運用簡單的套件進行現代運算（第 … 閱讀全文
• 【Python】Insertion Sort 插入排序｜演算法介紹、新手快速入門
  目錄 基本概念實際應用線上學習平台推薦udemy推薦入門書籍精通 Python：運用簡單的套件進行現代運算（第 … 閱讀全文
• 【Python】Selection Sort 選擇排序｜演算法介紹、新手快速入門
  目錄 基本概念實際應用線上學習平台推薦udemy推薦入門書籍精通 Python：運用簡單的套件進行現代運算（第 … 閱讀全文

• Facebook
• Instagram
• Twitter