• Facebook
• Instagram
• GitHub

前言

上次寫完 【Python】Stack(堆疊) 資料結構實作 得到了不錯的迴響

這是要來寫寫有關 Binary Search Tree (二元搜尋樹)

希望大家不要聽到有關「Tree」的資料結構就望而生畏

且聽我在此娓娓道來

本篇文章會帶到以下幾點有關Binary Search Tree該知道的事：

1. BST 的 基本概念
2. BST 的 Big-O
3. Python 實作 BST （加入 node & 印出 tree

你可能會喜歡：【2020】我的Python學習心路歷程

二元樹基本概念

二元樹就是由多個node組成

而BST就是以 node-based 為基礎的資料結構，當中要注意到BST有以下幾點特性：

1. node左子樹只會包含比本身還要小得值
2. node的右子樹只會包含比自己大的node
3. 每個左右子樹都要是二元搜尋樹
4. 不可以有值重複的 node

BST Big-O

	Average	Worst Case
Space 空間	Ｏ(n)	Ｏ(n)
Access 存取	O(log n)	Ｏ(n)
Search 搜尋	O(log n)	Ｏ(n)
Insertion 加入資料	O(log n)	Ｏ(n)
Deletion 刪除資料	O(log n)	Ｏ(n)

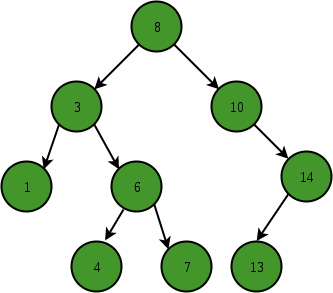
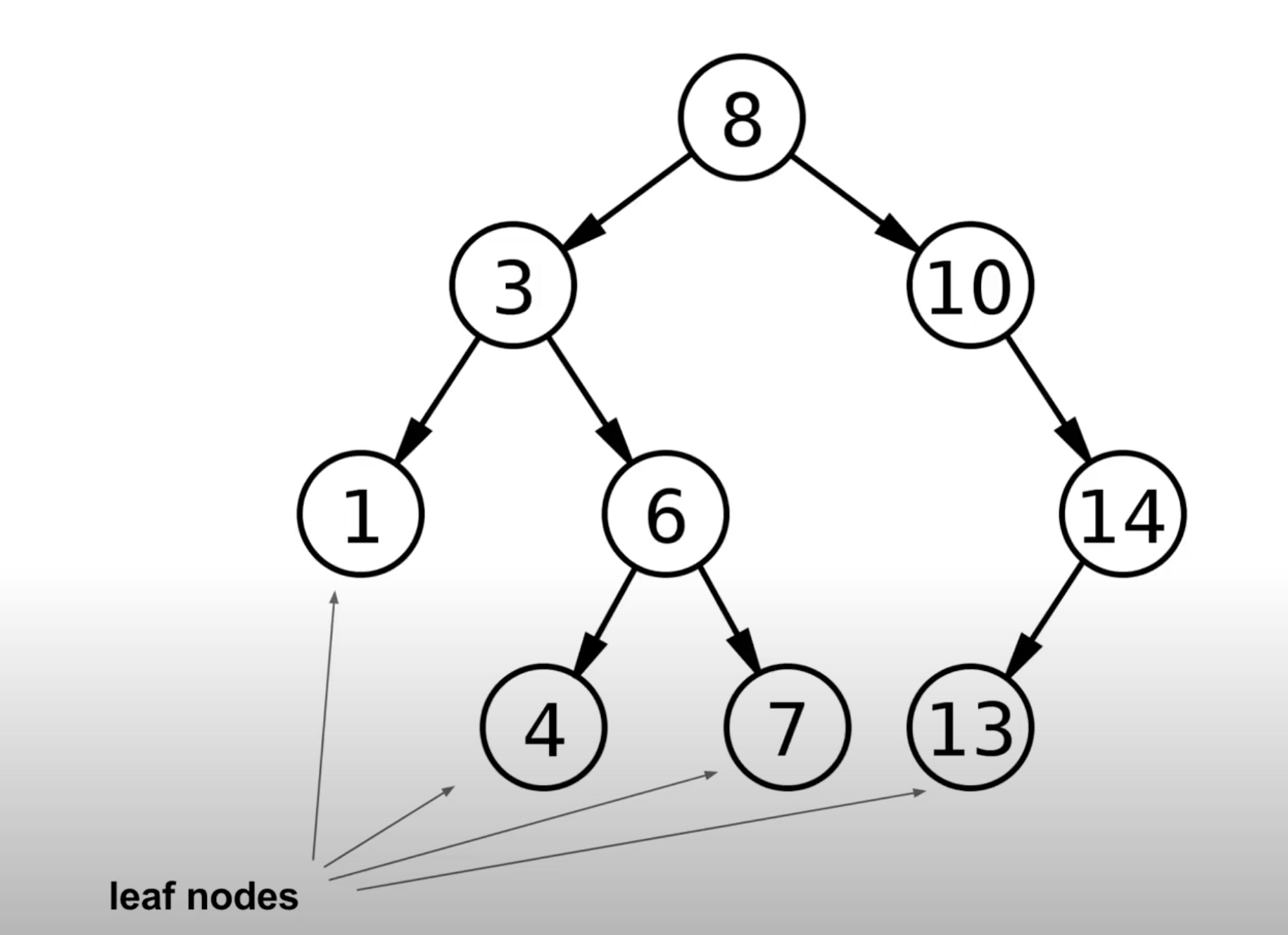
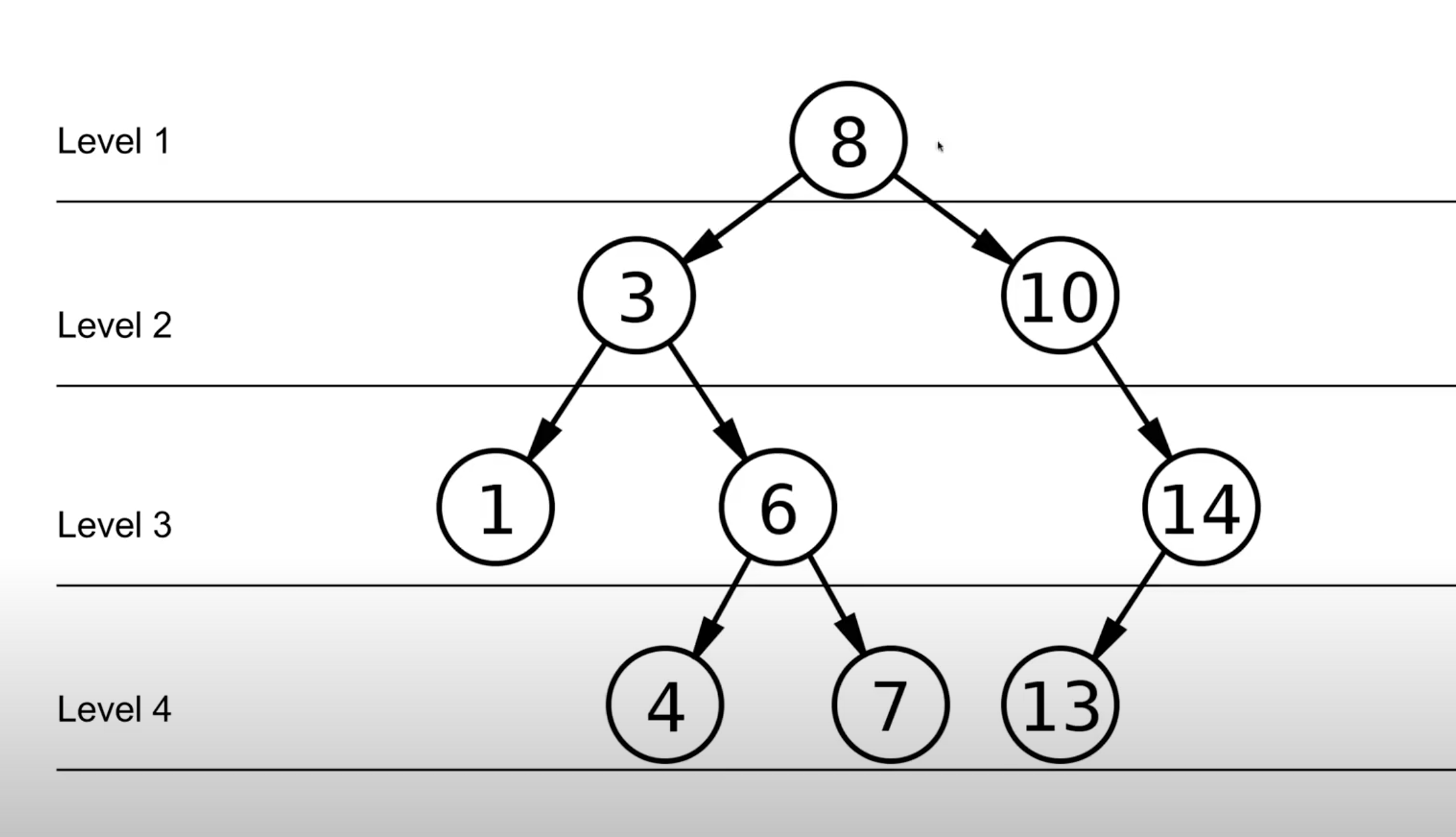
ex: Level 4 的Binary tree 最多可以有 2^4 - 1 = 15 個 node

以上的二元搜尋樹提供了node之間的順序，因此可以快速完成搜索，最小，最大等操作。如果沒有排序，我們就必需比較所有的鍵(key)來搜尋給定的鍵

Full Binary Tree

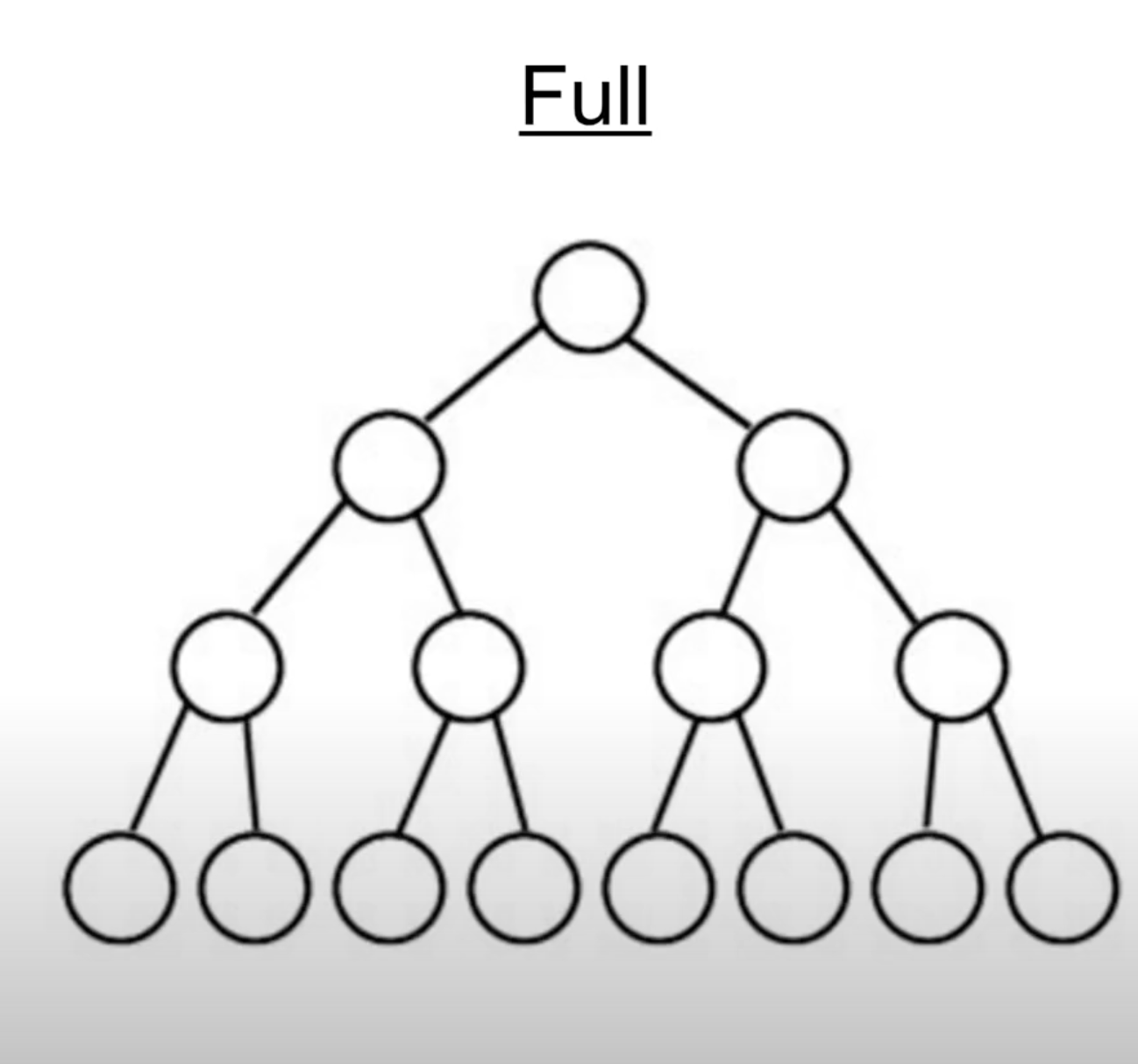
• 所有node都有兩個subtree 子樹 (也就是兩個child pointer)；
• 所有leaf node具有相同的level(或相同的height)
• 計算結點數公式為：2^n - 1

ex: Level 4 的 Full Binary tree 一定有 2^4 - 1 = 15 個 node

Complete Binary Tree

一棵樹的node按照Full Binary Tree的次序排列(由上至下，由左至右)，則稱此樹為Complete Binary Tree

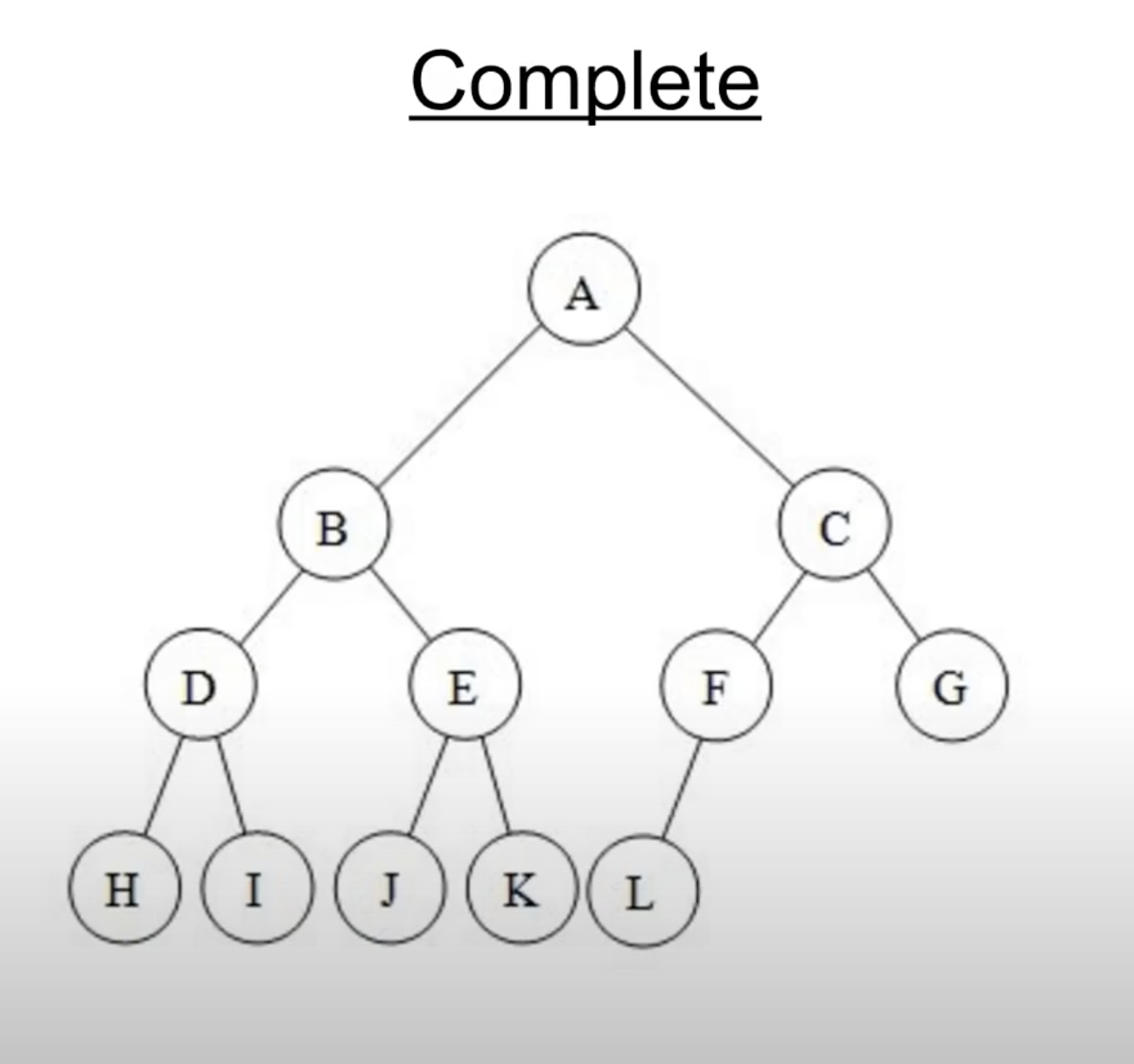
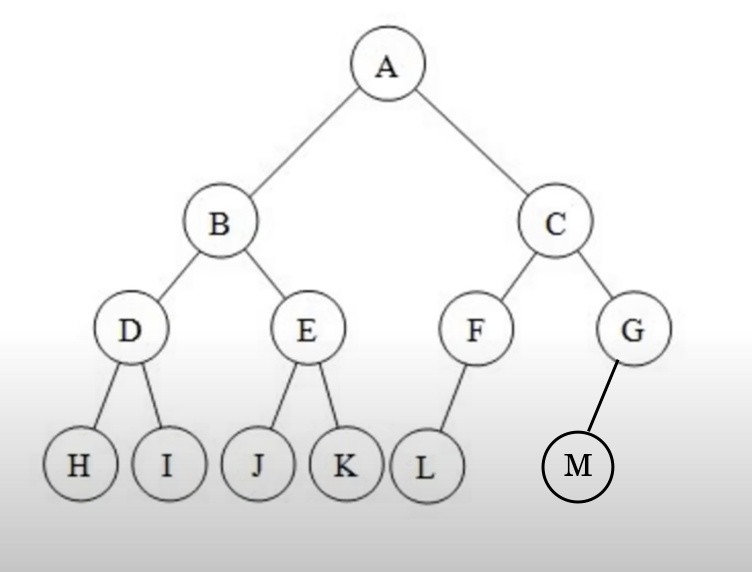
圖6 Node(Ｍ)應該要移到 Node(F)的右子樹，因此下圖並沒有滿足Complete Binary Tree的特性

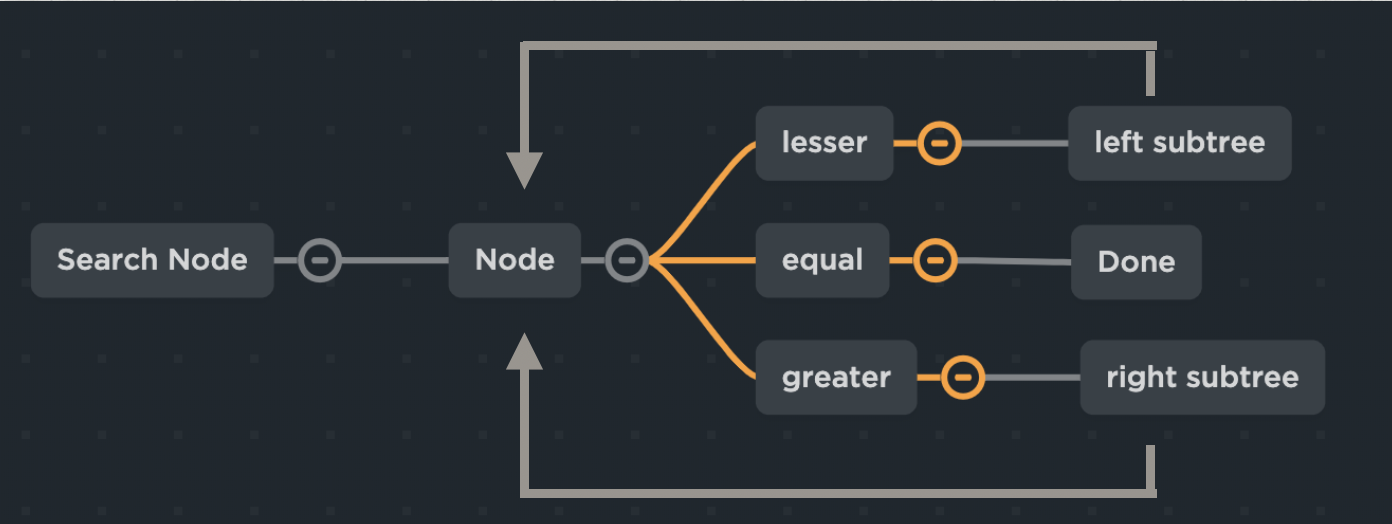
搜尋二元樹

數一定是從root開始找起，不論是刪除，新增等等

我們將從一個'n'個節點的搜尋Space開始，當我們丟棄(discard)一個子樹時，我們將丟棄'n / 2'個節點，因此我們的搜索Space將減少為'n / 2'個，然後在下一個步驟我們將搜索空間減少到'n / 4'，然後繼續像這樣減少直到找到元素(element) 或直到我們的搜尋減少到一個節點（node）為止

新增node

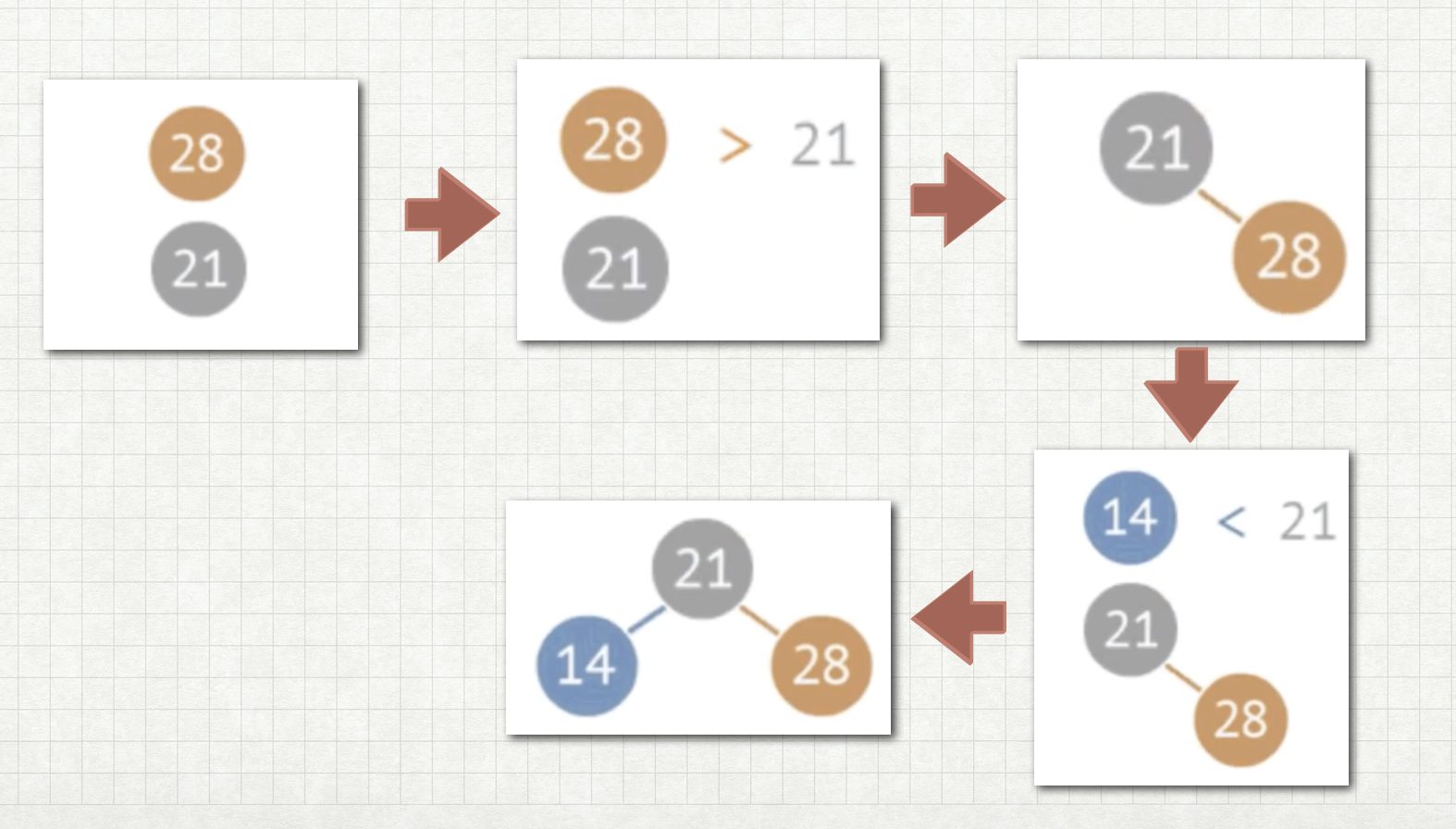
由圖8可知 Node 會先比較 目前的node 如Node(21)

當Node(28) 大於 Node(21) 且 Node(21) 沒有右子樹時 Node(21) 的 右子樹 就會指向 Node(28) 以此類推

你可能會喜歡：【Python】Stack(堆疊) 資料結構實作

Python 實作 BST 二元搜尋樹

首先我們要先建立2個class來讓二搜尋樹動起來

我們要先建立一個 Class Node

將 instructor初始化

一個 node 可以儲存 value ，還有指向 left_child 和 right_child 初始化都指向 None (因為都還沒有資料)

class Node:
    def __init__(self, value=None):
        self.value = value
        self.left_child = None #smaller
        self.right_child = None #greater

接著要來正式建立 二搜樹的Class了

二搜樹的Class 就好像是 Node 的 wrapper

負責控制 Node 的資料＆該指向哪裡

而這個概念同 Linked List Class Node 跟 Class LinkedList 的關係

建立Class binary_search_tree

同理，一開始二搜樹內是沒有資料的所以將 instructor 初始化為 self.root = None

class binary_search_tree(self):
    def __init__(self):
        self.root = None

接著我們創建一個 insert() 的function
顧名思義就是讓我們加入資料
插入資料前我們要先檢查樹是否為空 if self.root == None
如果 root == None 代表樹是空的
因此 value 就等於 self.root

如果 root != None 的話
我們就呼叫 private function _insert()
⚠️實際上Python沒有所謂「真正的」private function，所以如果我們看到 _<function_name> 的時候，我們要避免在 Class 外呼叫private_function

接著在這個 _insert() 內要傳入 value 和 root (我們正在查看的current Node)

為什麼要將一個function分成2個的原因是 _insert() 是 「遞迴的」用「一個function 來處理遞迴的事情」 會比 「讓所有邏輯處理都塞在 insert() 」裡來的好

class Binary_search_tree:
    def __init__(self):
        self.root = None

    def insert(self, value):
        #判斷tree是否為空
        if self.root == None:
            self.root = Node(value)
        else:
            self._insert(value, self.root)

接著我們開使寫 _insert() 的 function
就像剛剛說的，在 _insert() 裡傳入 value 和 cur_node
而上面 self._insert(value, self.root) 傳入 root的原因是因為所有要新增的Node一定要經過 root

接下來我們就能開始比較「傳入的value 是否 大於 cur_node」了
再來，我們要分成兩個狀況
當 value < cur_node （value小於目前的node）
如果 cur_node.left_child == None 也就是目前的node「沒有」指向 left_child 的 pointer
理所當然 cur_node.left_child = Node(value)
如果 cur_node.left_child != None 也就是目前的node「有」指向 left_child 的 pointer
我們會把 left_child 當成 cur_node 並重新呼叫 _insert()

right_child 同理

最後 else 要處裡 value 與 cur_node 的 value相同的問題前面有提到，二搜樹的value是不能重複的

   def _insert(self, value, cur_node):
        if value < cur_node.value:
            if cur_node.left_child == None:
                cur_node.left_child = Node(value)
            else:
                self._insert(value, cur_node.left_child)
    
        elif value > cur_node.value:
            if cur_node.right_child == None:
                cur_node.right_child = Node(value)
            else:
               self._insert(value, cur_node.right_child)
                    
        # value == cur_node.value
        else:
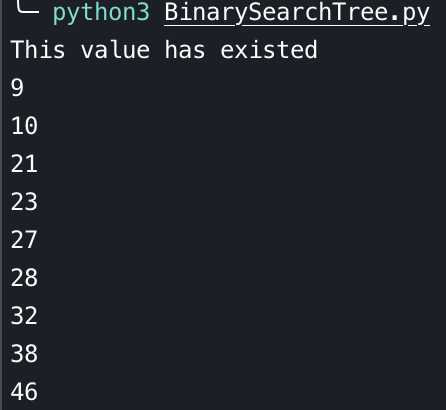
            print("This value has existed")

你可能會喜歡：【2020】我的Python學習心路歷程

終於要把樹印出來了（茶
我們先檢查 self.root 是不是 Node
如果 self.root != None （也就是 self.root 有值
我們呼叫 _print_tree(self.root)
同理一樣是用「遞迴」的方式處理，所以將它寫成private function

def print_tree(self):
        if self.root != None:
            self._print_tree(self.root)

同樣印出一棵樹也是從root開始查找
所以cur_node設為self.root
所以 _print_tree(self, cur_node)

  def _print_tree(self, cur_node):
      if cur_node != None:
          self._print_tree(cur_node.left_child)
          print(str(cur_node.value))
          self._print_tree(cur_node.right_child)

最後在class外建立一個 function來幫我們自動建立一個二搜樹

def fill_tree(tree, num_elems=10, max_int=50):
    from random import randint
    for _ in range(num_elems): #10個 value
        cur_elem = randint(0, max_int) #隨機0~50(不含50)的值
        tree.insert(cur_elem)
    return tree

tree = Binary_search_tree()
tree = fill_tree(tree)

tree.print_tree()

執行結果

Python BST 完整程式碼

GitHub: https://github.com/LichtLiu/PG_Data_Structure/blob/main/Binary%20Search%20Tree/BinarySearchTree.py

class Node:
    def __init__(self, value=None):
        self.value = value
        self.left_child = None #smaller
        self.right_child = None #greater

class Binary_search_tree:
    def __init__(self):
        self.root = None

    def insert(self, value):
        #判斷tree是否為空
        if self.root == None:
            self.root = Node(value)
        else:
            self._insert(value, self.root)

    def _insert(self, value, cur_node):
        if value < cur_node.value:
            if cur_node.left_child == None:
                cur_node.left_child = Node(value)
            else:
                self._insert(value, cur_node.left_child)

        elif value > cur_node.value:
            if cur_node.right_child == None:
                cur_node.right_child = Node(value)
            else:
                self._insert(value, cur_node.right_child)

        # value == cur_node.value
        else:
            print("This value has existed")

    def print_tree(self):
        if self.root!=None:
        	self._print_tree(self.root)

    def _print_tree(self,cur_node):
    	if cur_node!=None:
        	self._print_tree(cur_node.left_child)
        	print(str(cur_node.value))
        	self._print_tree(cur_node.right_child)


def fill_tree(tree, num_elems=10, max_int=50):
    from random import randint
    for _ in range(num_elems): #10個 value
        cur_elem = randint(0, max_int) #隨機0~50(不含50)的值
        tree.insert(cur_elem)
    return tree

tree = Binary_search_tree()
tree = fill_tree(tree)

tree.print_tree()

結語

二元樹一直以來是大公司非常注重的觀念之一
想必他在資料結構上有舉足輕重的地位
一定要花時間好好學習
想必在此之後對程式撰寫邏輯上會有莫大的幫助

本篇只有探討到 新增資料 與 印出資料
日後會再補上 刪除與搜尋function
敬請期待

如果對文章內容有任何問題，歡迎在底下留言讓我知道。 
如果你喜歡我的文章，可以分享我的文章，讓更多的人看見我的文章。 
追蹤我的Instagram，看我分享 #咖啡 #Python
如果這篇文章對你有幫助，
可以幫我在下方按 5 個Like 讓我得到一些回饋，
支持我繼續寫出更多好文章！

  
 
 
 
 
 
 
 View this post on Instagram
 
 
 
 
 
 
 
 
 
 
 🐧分享我最愛用的幾個app 1. ClickUp —>專案管理大推 2. Sourcetree —> Git GUI 3. GitHub —> 一定要會用的 4. Atom —> 目前愛用的code editor 5. Iterm2 —> 終於不是死板的Terminal #愛喝咖啡 #咖啡程式 #咖啡程式吱喳 #code #programmer #programming #atom #clickup #sourcetree #github #iterm2 #workspace #application #computer #computerscience #engineer #engineering #coding #codinglife💻
 
A post shared by  🇹🇼咖啡程式人Joy (@lovedrinkcafe) on Nov 6, 2020 at 5:28pm PST
 

• 【SSH】製作SSH key教學
• 【快速架站】什麼是Hexo? 5分鐘快速架站教學
• 【Python】Quick Sort 快速排序｜演算法介紹、新手快速入門
• 【Python】Insertion Sort 插入排序｜演算法介紹、新手快速入門
• 【Python】Selection Sort 選擇排序｜演算法介紹、新手快速入門
• 【Python】Bubble Sort 泡沫排序｜演算法介紹、新手快速入門
• 【Python】Binary Search 二分搜尋｜演算法介紹、新手快速入門
• 【Python】linear search 線性搜尋｜演算法介紹、新手快速入門
• 【Python】什麼是演算法？｜演算法介紹、新手快速入門
• 【教學】使用Sourcetree將專案push到Github｜GitHub Token 產製與用法

• Facebook
• Instagram
• GitHub